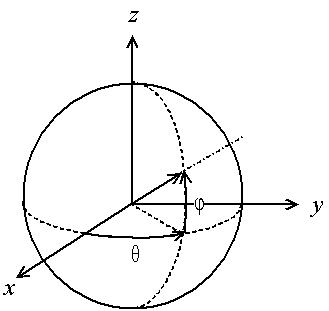
Fig. 2.1 - Repérage en coordonnées polaires dans l'espace
Soit une fonction ƒ(θ, φ) -- il s'agit là de coordonnées polaires habituelles.

Fig. 2.1 - Repérage en coordonnées polaires dans l'espace
ƒ(θ, φ) = ∑l = 0∞ ∑m = -l+l Clm.Ylm(θ, φ)Clm étant un coefficient. Les fonctions Ylm(θ, φ) présentent de plus en plus de symétries au fur et à mesure que l croît (sauf lorsque l =0, puisque Y00 est une fonction constante et décrit donc une sphère). Lorsque θ et φ décrivent [0;2π[, Ylm(θ, φ) s'annule selon l cercles :
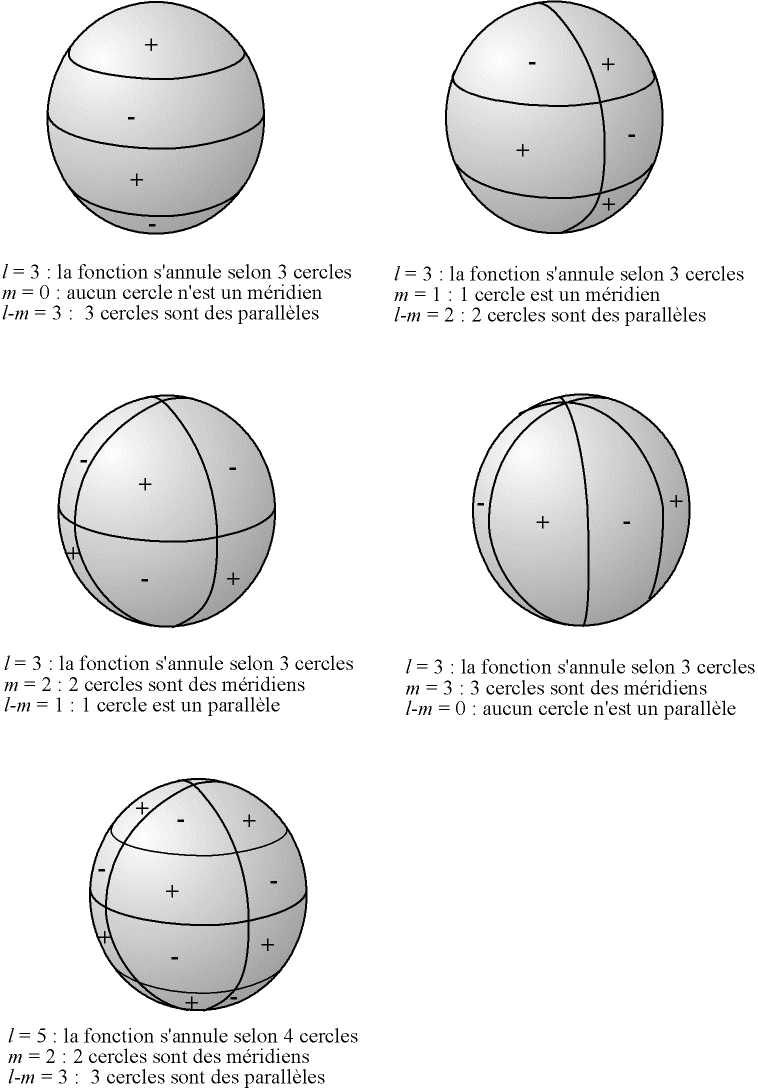
Fig. 2.2 - Cercles d'annulations d'une harmonique sphérique
Nous représentons ci-dessous la fonction r0 + r1.Y32(θ, φ), avec 0 < r1 < r0, selon quatre plans de coupe (deux parallèles et deux méridien), les cercles en pointillé figurant les traces de la sphère de rayon r0.
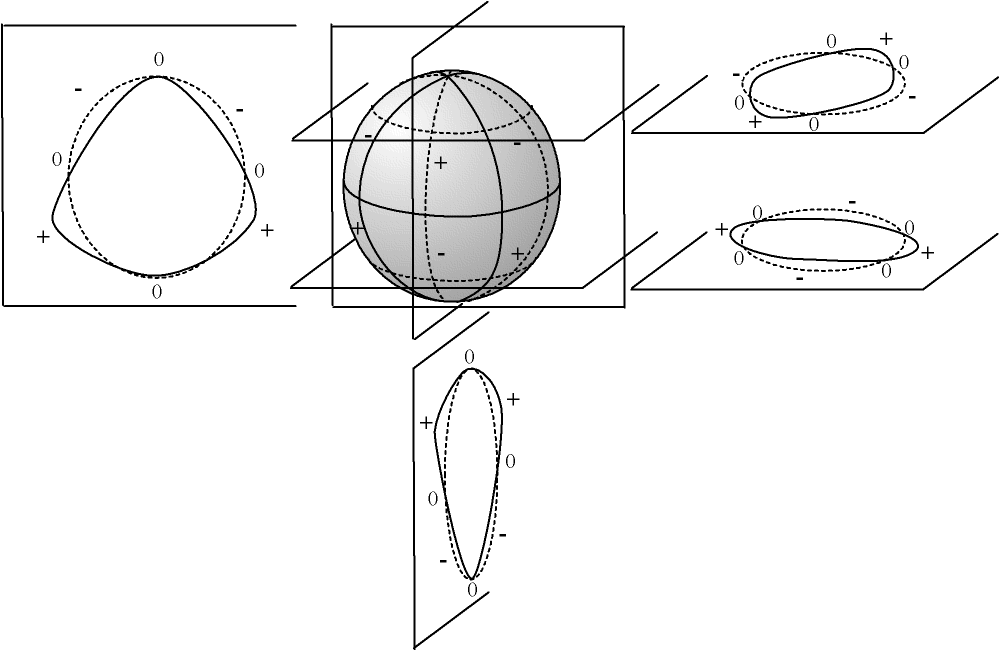
Fig. 2.3 - Traces d'une harmonique sphérique
On représente également souvent |Ylm(θ, φ)|² ; par exemple, ci-dessous, |Y00(θ, φ)|², |Y10(θ, φ)|² et |Y20(θ, φ)|² :
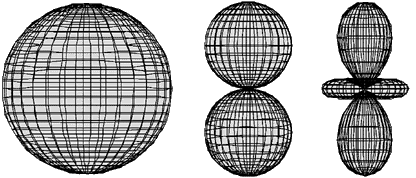
Fig. 2.4 - Représentation de |Ylm(θ, φ)|2
Une fonction ƒ(θ, φ) peut donc se décomposer en une somme de fonctions Ylm(θ, φ).
| début |
Les harmoniques sphériques utilisées au § 2.1 sont en fait les parties réelles des harmoniques sphériques complexes Ylm(θ, φ). La fonction Ylm(θ, φ) peut s'écrire comme le produit d'un polynôme Plm en cosinus de θ, appelé «fonction associée de LEGENDRE», et d'une exponentielle complexe en φ :
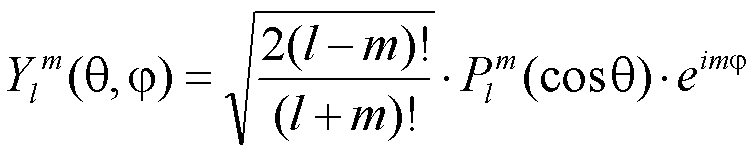
avec
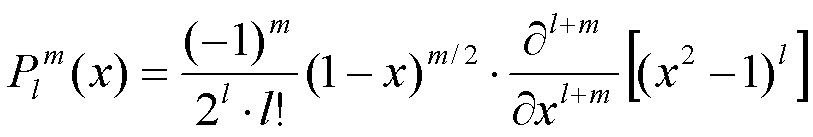
par exemple :
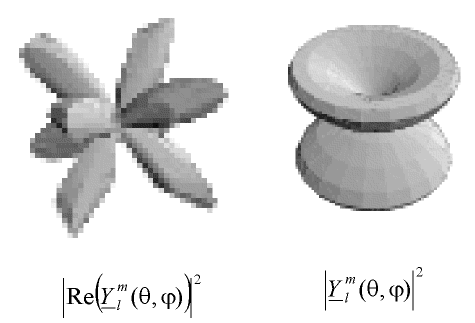
Fig. 2.5 - Représentation de la norme de la partie réelle
et de la norme elle-même
de Y32(θ, φ)